 Stumped?
Stumped?It's not a trivial problem, is it? It turns out, however, that it is possible to do and an ancient Greek named Eratosthenes (c. 276 BCE - c. 195 BCE) figured it out (Eratosthenes really was a polymath - Wikipedia describes him as a Greek mathematician, geographer, astronomer, music theorist, and poet who, given the size of his head, must have been brilliant!). Critics nicknamed him Βήτα ("Beta" - the second letter of the Greek alphabet) because, while knowledgeable about everything, he was always seen as being second-best. Supporters, however, called him Πένταθλος, ("pentathlos") a word used to describe well-rounded athletes who performed well in all events.
Born in Cyrene (in Libya, today, but part of the lands conquered by Alexander the Great and a Greek city), Eratosthenes was undoubtedly recognized for his intelligence as a youth since he was sent to Athens to continue his education where he ended up studying with several famous Greek philosophers and poets. At 30 years old, his writings on poetry and history captured the attention of the Pharaoh who invited him to work at the Library of Alexandria (the most famous library of the ancient world and a center of learning - think of being invited to work at Oxford or Harvard today). He spent the rest of his life there becoming Chief Librarian after just five years. He was held in such high esteem that he tutored the children of the Pharaoh (one of whom became the next Pharaoh). Eratosthenes was a also good friends with Archimedes (another brilliant Greek).
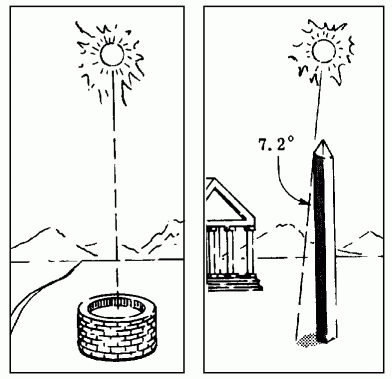
Back to the size of the Earth. It turns out the Eratosthenes knew about a well in the Egyptian city of Syene (called Aswan today) that had an interesting feature. On the day of the summer solstice (the longest day of the year when the Sun rises and sets in its most northerly positions), the Sun would illuminate the bottom of the well at local noon. In other words, on the solstice, and only on the solstice, the Sun was directly over this well in Syene.
Looking down into the well at Syene
Today, we know why this occurred at Syene. The Earth is tilted by 23.5° and, on the summer solstice, the Northern Hemisphere is at it's maximum tilt toward the Sun. At local noon, the Sun will be directly over 23.5° N latitude (the Tropic of Cancer). Syene (now called Aswan) is located very close to that latitude.
In the north of Egypt, Eratosthenes also knew that on the summer solstice, the Sun was not directly overhead in Alexandria where he was located. How could you explain the fact that the east-west moving Sun was directly over one city on a specific day but not directly over another city, further to the north, at the same time?
Alexandria and Syene (note they're not quite on the same N-S meridian)
Well, one hypothesis which would explain this observation is that the Earth is spherical. "Wait," you might be thinking, "didn't ancient people believe the Earth was flat?" If you go back to the Mesopotamian world view, and the Biblical world view that arose from that, the answer is yes. As a digression, any literal reading of the Torah/Psalms/Prophets (Old Testament) clearly indicates the world is fixed, the center of the universe, and flat with corners and pillars (just as clearly as the view held by some supposedly modern religious groups that the Earth is only a few thousand years old and all life was saved by Noah and his ark).
By the time of the ancient Greeks, however, some intelligent people were wondering if the Earth might not be spherical. Aristotle, who live 100 years before Eratosthenes, even proposed several logical arguments in support of a spherical Earth (one argument, for example, was that one saw stars in the southern sky in Alexandria, Egypt that were below the horizon in Athens on the other side of the Mediterranean. By similar reasoning, the Sun could be overhead in Syene yet not quite exactly overhead in Alexandria.
One easy way to measure the angle of the Sun at noon is to use the shadow cast by a tall, straight object. If the Sun is directly overhead, no shadow will be cast but if it's not quite overhead, a shadow will appear. So what can you use for a tall, straight object? Well, Eratosthenes was in Egypt - how about an obelisk like Cleopatra's Needle?
Painting of an obelisk in Alexandria (Cleopatra's Needle) circa 1850
Another brilliant Greek, Euclid, who also lived about 100 years before Eratosthenes, developed the mathematical field of geometry which can be used to calculate the angle between the Sun and the zenith (the point in the sky directly overhead) from the known height of the obelisk and the measured length of the shadow cast.
The well at Syene (left) and obelisk in Alexandria (right) at the summer solstice
The angle of the Sun's rays from vertical turned out to be 7.2°. According to Euclid's geometry, this will be the same as the angle formed between lines connecting the center of the Earth to both Alexandria and Syene. Eratosthenes also knew, by talking to Egyptian surveyors, that the distance from Alexandria to Syene was about 5,000 stadia. There is some debate as to the length of a stadion at the time but I'll use the conversion of 1 stadion = 150 meters (0.15 km).
Now, since 7.2° is to 360° (the number of degrees around a circle) as 5,000 stadia is to the circumference of the Earth (C), we can set up the equation:
(7.2° / 360°) = (5,000 stadia / C)
C = (5,000 stadia * 360° / 7.2°)
C = 250,000 stadia
Converting to kilometers:
250,000 stadia * (0.15 km/stadion) = 37,500 km
The modern value for the circumference of the Earth is 40,070 km so Eratosthenes would have only been off by 6.4%. That's pretty damn good for something done over 2,000 years ago!
There are a few sources of error in this value. Eratosthenes assumed Alexandria and Syene were directly lined up with each other in a north-south direction. They're not (see the map above). The value for the distance from Alexandria to Syene was not exact. A tenth of a degree difference in the measured angle leads to a difference of thousands of stadia in the final result. And, finally, we're not sure of the exact conversion between an Greek stadion of 200 BCE and a modern kilometer.
As a final note, when Christopher Columbus proposed to go after the spices of India by sailing west across the Atlantic, he knew the Earth was round. King Ferdinand's advisers counseled him to turn down Columbus's proposal because Eratosthenes estimate for the size of the Earth gave an untenable distance going that way around. Columbus, however, argued persuasively enough that this value was too high and convinced Queen Isabella to give him a shot. The rest, as they say, is history.
Now that the size of the world had been measured, I'll explain in my next post how it was weighed.






No comments:
Post a Comment