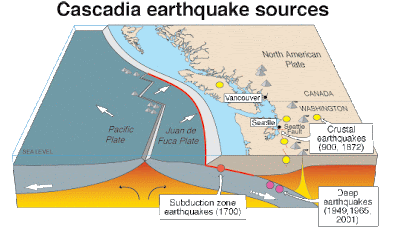
As Plait says "Post script: can you imagine a show like this running on American TV? No, I can’t either..." God forbid, with 100+ cable channels, there should be some intelligent program material (which I why I don't even subscribe to cable TV).
In my introductory science classes, I like to explain to students how atoms are really small, mostly empty space, and not at all like they commonly imagine.
Let's look at the size of a typical atom. Nothing is more typical than hydrogen - the most abundant element in the known universe. Hydrogen is simple - it's just one negatively charged electron orbiting a positively charged proton (let's ignore electrically-neutral neutrons for now).
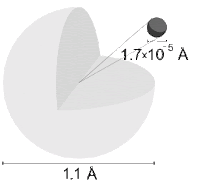
Below left is a simple model of a hydrogen atom. This type of model is called the Bohr model after Danish physicist Niels Bohr. While this is how most people visualize atoms - as hard, little electrons orbiting a nucleus like planets around a star - it's completely incorrect as a physical model. We'll come back to that in a bit.
Above right is an image from Wikipedia showing the diameter of the proton in a hydrogen atom (1.7 x 10-5 Å) and the diameter of the atom itself which is the orbital shell of the electron (1.1 Å).
For those of you unfamiliar with angstroms (Å), one angstrom is equivalent to 10-10 meters.
Why no diameter for the electron? Well, it's complicated and physicists generally treat it as a point charge. We can say that the mass of the electron is 1,836 times smaller than the mass of a proton, however. That's like comparing my weight to something weighing 2 ounces.
Now, let's look at the relative sizes of the nucleus and orbital shell for a hydrogen atom.
(1.1 Å / 1.7 x 10-5 Å) = 64,706
In other words, in a hydrogen atom, the electron orbital is 64,706 times the diameter of the proton in the nucleus. Let's make that easier to visualize. Image we blow up the proton to the size of a golf ball. Wikipedia gives the minimum diameter of a golf ball as 43 mm or 4.3 x 10-2 m.
[(1.7 x 10-5 Å) / (4.3 x 10-2m)] = [(1.1 Å) / X]
X = [(1.1 Å) (4.3 x 10-2m) / (1.7 x 10-5 Å)]
X = 2,782 m
Divide diameter by 2 for the radius = 2,782 m / 2 = 1,391 m
That's 1.4 km or 0.9 miles. In other words, if the proton nucleus of a hydrogen atom were the size of a golf ball, the electron would be orbiting almost a mile away! That's why we say atoms are mostly empty space!
Atoms are also really, really small. How small? Let's compare the size of a hydrogen atom to the size of a penny. Once again, Wikipedia to the rescue telling us that a U.S. penny is 19.05 mm in diameter (1.9 x 10-2 m).
(1.9 x 10-2 m / 1.1 x 10-10 m) = 172,727,273
A penny is 173 million times the diameter of a hydrogen atom! How big is a penny if we blew it up 173 million times?
1.9 x 10-2 m x 172,727,273 = 3,281,818 m = 3,281 km
For reference, the diameter of the Moon 3,475 km. Let's suppose a careless astronaut dropped a penny on the surface of the Moon. The size of that penny compared to the Moon is about the same as the size of a hydrogen atom compared to a penny!
Back now to the Bohr model of the atom. The image of electrons orbiting a nucleus like the image at left is useful for understanding how atoms bond, it really does give us the wrong idea.
The modern, quantum mechanical model of an atom has variously-shaped electron "clouds" around the nucleus with electrons essentially behaving as waves. Electrons can only occur in certain orbitals because they're essentially like standing waves as Brian Cox explains in the video. To really understand this, you have to understand the mathematics of the Schrödinger equation.
Reality gets very strange at the atomic scale!