by Siobhan Roberts (2006, Walker & Company) when I saw it in the new books area of my college library.I had never heard of Harold Scott MacDonald "Donald" Coxeter (1907-2003), but he was evidently well known as a classical geometer in the mathematical community. Born and educated in England (Trinity College, Cambridge), he spent 60 years of his professional life at the University of Toronto in Canada.
Everyone is familiar (or should be) with the the classical geometry of Euclid developed around 300 BCE and which ruled for some 2,000 years in mathematical education.
Less familiar to most are the non-Euclidean geometries developed in the 19th century by mathematicians such as János Bolyai, Nikolai Lobachevsky, and Bernhard Riemann. Geometries which grew out of playing with Euclid's parallel postulate. As a simple example, think of how geometry on the surface of a sphere would be different from planar geometry on a flat sheet of paper - on a plane the three interior angles of a triangle add up to 180° and on a sphere they add to more than 180°.
In the 20th century, geometry fell out of fashion in mathematics, especially the more visual and intuitive forms of geometery that interested people like Donald Coxeter (and many amateur mathematicians). One group of influential French mathematicians, who published collectively under the pseudonym of Nicolas Bourbaki, argued against mathematical intuition, stressed rigor and formalism, and famously exclaimed "Death to triangles!" in reaction to the constructions of classical geometry.
Donald Coxeter swam against the mathematical tide and followed his passion, even when advised by colleagues to quit messing around with circles and triangles and move into more "important" mathematical areas. Turns out, however, that many of the things Coxeter was interested in are important and useful.
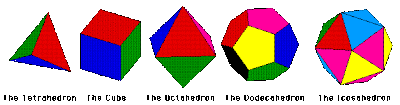
One topic that Coxeter found interesting are regular polytopes. These are generalization into higher dimensions of objects like the five Platonic solids known to the ancient Greeks (the tetrahedron, cube, octahedron, dodecahedron, and icosahedron). While mathematicians find such shapes irresistable to explore, there are useful applications when looking at symmetry in crystallography, molecular shapes, and dimensions in modern string theory.
While Coxeter was not all that exciting a personality, Siobhan Roberts does provide an interesting biography. Coxeter was a vegetarian (due to his poor digestive health) and pacifist (at a time such a view wasn't popular). He comes across as sympathetic even while being somewhat aloof and not a very good husband or father to his children (his wife commented that his mistress was mathematics).
One criticism I have of the book, however, is that the author doesn't seem to understand much of the mathematics she writes about (or, if she understands it, she isn't able to explain it well). There are many places where she discusses Coxeter's work, but in a very superficial way without the imagery I believe Coxeter himself would have included when explaining his research. I would like to have learned more about regular polytopes that I did reading this book. The book itself seems somewhat schizophrenic partly being a popular biography of an interesting character and partly attempting to be a scholarly work (with 60+ pages of footnotes).
Finally, the book does have one interesting Hudson Valley link. George Odom, an artist and long-time resident of the Hudson River Psychiatric Center in Poughkeepsie, corresponded frequently with Coxeter for decades and sent Coxeter amazing numbers of geometric models he created (he evidently had a lot of free time in the psychiatric institute).
Overall, worth reading. Some parts I did find myself skimming, however.
No comments:
Post a Comment