Teaching math

I was in the doctor's office the other day, getting blood drawn, and the phlebotomist asked me what I was reading since I was carrying a book (I'd rather read when sitting in an examination room waiting for the doctor than stare at those charts of nasty medical illustrations on the walls and wondering which disease is eventually going to kill me).

I told him it was a book about math (which I'll review in a couple of days when I finish reading it).  He then asked if I taught math and I told him I was a geologist we talked for a bit.  He told me he was never very good at math (as most people will tell you if they see you reading a book about math for fun), and one his memories from a high school math class was his teacher yelling at the class - "You know why you kids do so badly on the test?  It's because you can't follow directions and that's what math is - following directions!"

He was done drawing my blood, so I didn't continue the conversation, but I was horrified that a math teacher would yell at his class like that.  Not because he yelled at the students - good for him, they probably deserved it and never followed instructions - but because he told them something I think is totally false.  Math, real math, is not simply "following directions".  I would contend just the opposite - that teaching math this way is the worst possible way to do it (to be fair, of course, I'm just going by some one's memory of a long-ago math class, reality may have differed).

Also keep in mind, in what follows, is that I'm not a math teacher.  I'm a geologist that likes math and think it's terribly interesting (I also find myself teaching elementary algebra to college students in my geology lab when they can't solve certain problems).  Take what I say with a grain of salt (perhaps a math teacher could chime in if they're reading this).

To be fair, a large part of math is "following directions" in that math has rules.  The plus sign + has a specific meaning in mathematics as an operation.  When doing something to one side of an equals sign, you also have to do the exact same thing to the other side.

The problem is when students reach college and think of math as simply a system of mysterious rules and formulas with zero understanding of how it all works.  That's why people always complain about "word problems" in math - if you don't understand the concepts, you can't apply them to solve a problem.

A concrete example.  Most people are aware that the Earth's rigid outer shell (called the lithosphere by geologists) is split into plates which drift around over geologic time.  This process is called plate tectonics and is central to modern science of geology.  The Pacific Ocean is mostly underlain by a plate called, not surprisingly, the Pacific Plate.

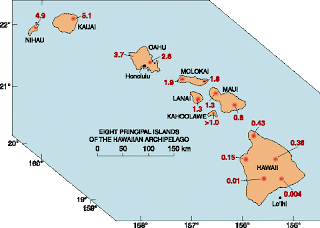
The Hawaiian Islands are in the middle of the Pacific Plate and formed from volcanic activity.  This is because that part of the plate is moving over a hot spot - a place where hot material is rising up through the mantle (a mantle plume) and generating magma at the base of the oceanic lithosphere (the "plate").  This magma erupts onto the seafloor and eventually builds up the volcanic islands we know as the tropical paradise of Hawaii.

The diagram below illustrates this.  The hot spot is currently under the Big Island and Hawaii and that's why volcanoes like Kilauea are still erupting there.  One million years ago, the Big Island didn't exist and Maui was over the hot spot.  From 1.1 to 1.8 million years ago, Molokai was over the hot spot.  From 2.2 to 3.3 million years ago, Oahu was over the hot spot.  You get the idea.  That's why old volcanoes on Oahu are extinct, they don't erupt anymore.  Oahu moved off the hot spot over two million years ago - there's no more heat and magma to initiate volcanic eruptions.

So, after students have had lectures on plate tectonics, volcanism, etc., we have a lab where students are given a diagram similar to that below (red numbers are ages of volcanic features in millions of years) and asked to calculate the approximate rate of plate movement, in cm/yr (plate movements are almost always reported in centimeters per year) for the Pacific Plate over the past 5 million years.

The first thing many students ask is "What formula do I use?"  This is like a word problem in math where all of the information is given, but some students have no idea what to do with that information because they don't really understand what they're doing.  Then I explain that they need to calculate the velocity of the plate and ask them how velocity is defined.  We finally get to the fact that it's distance divided by time (cm/yr in our plate movement example).

Then some students will proceed to measure the distance from Hawaii to Kauai using the scale bar shown on the map and get a distance of about 550 km or so.   Then they'll divide that by 5,000,000 years and get an answer of 0.00011 cm/yr.  Other students will divide 550 km by 5 million years and get an answer of 110 cm/yr.  Nope, sorry to both, you completely ignored your units and got incorrect answers.  Very common.

The answer, of course, requires you to convert 550 km into centimeters (55,000,000 cm) and 5 million years into 5,000,000 years and then divide to get 11 cm/yr.  If I had simply posed the problem as "Find the distance in centimeters and the time in years and use the formula Rate = Distance / Time, they'd have no problem.  But, when the problem is left more vague, and relies on the understanding that rate is distance over time and that you have to pay attention to your units, many supposedly college-level freshman science majors fall apart.

Why?  Where's the disconnect?  I don't know.  I also get students who multiply instead of divide when working with map scales on topographic maps and tell me that the distance between features within Ulster County is millions of kilometers!  No number sense at all.

Another advantage of home schooling compared to public schooling (my wife and I homeschool our kids).  If they tell us "I don't understand word problems" we'll just concentrate on giving them word problem after word problem until they get it.  In public schools, once you're lost it's likely you'll remain lost.